Hyperfocale
Ear78, dans l'un des longues dicussions qui sont en train de se dérouler, tu conseilles d'utiliser l'hyperfocale en paysage.
Existe-t-il un tableau particulier au CZ 16-80 et l'A700 ? Sinon, comment fait-on le calcul pour chacune des valeurs d'ouverture et de focale ? Je crois que l'on se réfère au cercle de confusion. Où le trouver ?
Merci...
Existe-t-il un tableau particulier au CZ 16-80 et l'A700 ? Sinon, comment fait-on le calcul pour chacune des valeurs d'ouverture et de focale ? Je crois que l'on se réfère au cercle de confusion. Où le trouver ?
Merci...
-
Nekhro - Messages : 880
- Photos : 1
- Inscription : 04 Fév 2007
- Localisation : Viiliers-sous-Grez, 77
- Contact :
Pour le diamètre du cercle de confusion il faut utilser la taille du capteur en micromètres et sa taille en nombre de pixel.
Je prends l'exemple de la bible "La pratique du réflex numérique".
capteur de taille 22,2 x 14,8 mm - en pixels 3456 x 2304
On prend la mesure d'un des côtés du capteur (ici 22,2 mm) et on la converti en micromètres (22 200) et on la divise par le nombre de pixel sur ce même côté (ici 3456)
22200 / 3456 = 6,42 micromètres
Pour le diamètre du cercle de confusion il faut mulitplier par deux ce résultat, on obtient donc 12,84 micromètres soit 0,01284mm
Pour l'hyperfocale, la formule est
hyperfoclae = (focale x focale) / (ouverture x diamètre du cercle de confusion)
le résultat est en mm
Je prends l'exemple de la bible "La pratique du réflex numérique".
capteur de taille 22,2 x 14,8 mm - en pixels 3456 x 2304
On prend la mesure d'un des côtés du capteur (ici 22,2 mm) et on la converti en micromètres (22 200) et on la divise par le nombre de pixel sur ce même côté (ici 3456)
22200 / 3456 = 6,42 micromètres
Pour le diamètre du cercle de confusion il faut mulitplier par deux ce résultat, on obtient donc 12,84 micromètres soit 0,01284mm
Pour l'hyperfocale, la formule est
hyperfoclae = (focale x focale) / (ouverture x diamètre du cercle de confusion)
le résultat est en mm
Pour l'A700, le cercle de confusion est plus précisément :
23500/4288 * 2 = 10.96 µm = 0,01096 mm
Tiens, d'ailleurs, pourquoi on multiplie par 2? On de devrait pas plutôt diviser par 2 pour avoir un cercle de confusion inférieur à un pixel ?
Sinon, en multipliant par 2, le cercle de confusion s'étend sur 2 pixels induisant un léger flou ? (j'espère que le cercle de confusion n'est pas dans mon esprit )
)
23500/4288 * 2 = 10.96 µm = 0,01096 mm
Tiens, d'ailleurs, pourquoi on multiplie par 2? On de devrait pas plutôt diviser par 2 pour avoir un cercle de confusion inférieur à un pixel ?
Sinon, en multipliant par 2, le cercle de confusion s'étend sur 2 pixels induisant un léger flou ? (j'espère que le cercle de confusion n'est pas dans mon esprit
-
Nekhro - Messages : 880
- Photos : 1
- Inscription : 04 Fév 2007
- Localisation : Viiliers-sous-Grez, 77
- Contact :
Urgon a écrit :Tiens, d'ailleurs, pourquoi on multiplie par 2? On de devrait pas plutôt diviser par 2 pour avoir un cercle de confusion inférieur à un pixel ?
Sinon, en multipliant par 2, le cercle de confusion s'étend sur 2 pixels induisant un léger flou ? (j'espère que le cercle de confusion n'est pas dans mon esprit Laughing)
Bien non justement. Pour voir si un cercle est flou ou nette, il faut au moins 2 pixels, comme il faut plusieurs pixels pour composer une image. On ne peut pas dire si quelque chose est nette avec un seul pixel (encore moins avec 1/2).
Merci Nekhro.
Je me demande toutefois si Urgon n'aurait pas raison, car j'ai voulu vérifier le calcul en examinant un tableau donnant les distances hyperfocales d'un ancien bridge Canon. Le calcul ne tombe juste que si j'emploie une valeur de 0.006 mm qui semble plutôt être le rayon et non le diamètre du cercle de confusion ? A moins que les capteurs de ce temps là n'aient été vraiment beaucoup plus petits ?
Je me demande toutefois si Urgon n'aurait pas raison, car j'ai voulu vérifier le calcul en examinant un tableau donnant les distances hyperfocales d'un ancien bridge Canon. Le calcul ne tombe juste que si j'emploie une valeur de 0.006 mm qui semble plutôt être le rayon et non le diamètre du cercle de confusion ? A moins que les capteurs de ce temps là n'aient été vraiment beaucoup plus petits ?
-
Nekhro - Messages : 880
- Photos : 1
- Inscription : 04 Fév 2007
- Localisation : Viiliers-sous-Grez, 77
- Contact :
J'ai revérifié dans le bouquin et c'est bien le diamètre qui est utilisé, multiplié par deux parce qu'on utilise deux pixels.
As-tu calculé le diamètre du cercle de confusion du capteur de ton bridge à partir de sa taille et de son nombre de pixels ? Effectivement, les capteurs des bridges sont plus petits que ceux des réflexes, donc à nombre de pixels équivalents, les pixels seront plus petits.
Si je me trompe, que les ténors du forum me reprennent .
.
As-tu calculé le diamètre du cercle de confusion du capteur de ton bridge à partir de sa taille et de son nombre de pixels ? Effectivement, les capteurs des bridges sont plus petits que ceux des réflexes, donc à nombre de pixels équivalents, les pixels seront plus petits.
Si je me trompe, que les ténors du forum me reprennent
Je me permet de t'envoyer ici où tu trouveras toutes les formules nécessaires, en particulier dans le fichier OO ou XLS en bas de page.
Du plastique, du métal, du verre, beaucoup de piles en tout genre, et tout ça pour tâcher de faire des photos
http://perso.wanadoo.fr/photo-hh/
Ce qui me ravit : que 2 et 2 font 4 (merci à M. Desproges)
Ce qui m'exaspère : avoir compté 22 atouts à la fin d'une partie de tarot
http://perso.wanadoo.fr/photo-hh/
Ce qui me ravit : que 2 et 2 font 4 (merci à M. Desproges)
Ce qui m'exaspère : avoir compté 22 atouts à la fin d'une partie de tarot
En fait cette histoire de cercle de confusion qui depend de la taille du pixel n'est pas forcement la meilleur définition.
A la base (en argentique) le cercle de confusion est déterminé comme le pouvoir separateur de l'oeil sur un tirage d'une taille donné vu a une distance donné. On rammene ensuite la taille du tirage à la taille du support photographique et l'on a le cercle de confusion (30µm pour un 24x36).
Si on utilise cette définition le cercle de confusion ne depend pas du tout de la taille du pixel, mais uniquement de la taille du capteur (soit 20µm pour un aps-c). C'est d'ailleur assez logique pour celui qui regarde des tirage (a part si on colle le nez sur un grand tirage) car un tirage A4 venant d'un aps-c 6Mpx ou 12Mpx aurra la même zone de nettetée.
Maintenant pour le "pixel peeper" qui recherche la zone de netteté sur des crop 100% à l'écran, c'est en effet la taille du pixel qui va compter. On se retrouce avec des zones de netteté beaucoup plus reduite qu'en argentique.
A la base (en argentique) le cercle de confusion est déterminé comme le pouvoir separateur de l'oeil sur un tirage d'une taille donné vu a une distance donné. On rammene ensuite la taille du tirage à la taille du support photographique et l'on a le cercle de confusion (30µm pour un 24x36).
Si on utilise cette définition le cercle de confusion ne depend pas du tout de la taille du pixel, mais uniquement de la taille du capteur (soit 20µm pour un aps-c). C'est d'ailleur assez logique pour celui qui regarde des tirage (a part si on colle le nez sur un grand tirage) car un tirage A4 venant d'un aps-c 6Mpx ou 12Mpx aurra la même zone de nettetée.
Maintenant pour le "pixel peeper" qui recherche la zone de netteté sur des crop 100% à l'écran, c'est en effet la taille du pixel qui va compter. On se retrouce avec des zones de netteté beaucoup plus reduite qu'en argentique.
Pour qu'une image soit nette, il faut qu'un point sur le sujet donne un point sur le capteur (ou film). C'est ce qui se passe pour tout ce qui est dans le plan de mise au point, mais un point qui se trouve en avant ou en arrière formera un point devant ou derrière le plan du film/capteur. Comme le point image est le sommet d'un cône de lumière, le capteur coupe le cône, ce qui donne un cercle.
Tant que ce cercle ne déborde pas du pixel, on peut le confondre avec un point, l'image est nette.
S'il couvre plusieurs pixels, l'image est floue.
Le "diamètre critique" de ce cercle a donc un diamètre égal à 2 x le pas des pixels.
Le cône dont je parle plus haut est d'autant plus "pentu" (rapport Ø / L) que l'ouverture est grande et que le sujet est proche. Celà fait que l'écart de MAP qui rend l'image floue dépend directement de l'ouverture et inversement de la distance.
De là découle naturellement la notion de profondeur de champ et d'hyperfocale.
@Nekhro : il n'y a pas de "cercle net" dans l'histoire, et pour qu'un cercle soit net, il lui faudrait plus de 2 pixels !
Tant que ce cercle ne déborde pas du pixel, on peut le confondre avec un point, l'image est nette.
S'il couvre plusieurs pixels, l'image est floue.
Le "diamètre critique" de ce cercle a donc un diamètre égal à 2 x le pas des pixels.
Le cône dont je parle plus haut est d'autant plus "pentu" (rapport Ø / L) que l'ouverture est grande et que le sujet est proche. Celà fait que l'écart de MAP qui rend l'image floue dépend directement de l'ouverture et inversement de la distance.
De là découle naturellement la notion de profondeur de champ et d'hyperfocale.
@Nekhro : il n'y a pas de "cercle net" dans l'histoire, et pour qu'un cercle soit net, il lui faudrait plus de 2 pixels !
Fangio a écrit :Pour qu'une image soit nette, il faut qu'un point sur le sujet donne un point sur le capteur (ou film).
Pas du tout d'accord avec cette définition car elle pose selon moi 2 problèmes :
1) Cela supposerait qu'a nombre de pixels identiques 1 capteur 24x36 a une meilleure profondeur de champs qu'1 APS, or dans la réalité c'est l'inverse.
2) C'est oublier que la notion de flou n'est pas une notion physique (un point n'est pas une notion physique mais virtuelle) mais une notion liée à la perception qu'à la personne qui regarde l'image. les formules de calcul de profondeur de champ ne sont que la modélisation de cette impression et n'ont donc rien a voir avec la tailler des pixels.
Bref une zone de l'image est floue quand une personne ayant un oeil exercé et la regardant a bonne distance la juge floue (ce qui ce modélise). Le reste c'est du vent.
Dernière édition par nico le Ven 16 Nov 2007 12:51, édité 1 fois.
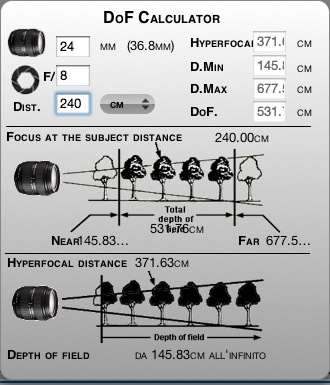
Moi je te dirais plus simplement d'employer le widget DoF Calculator si tu es sur Mac... 
Sinon tu as ce site
Sinon tu as ce site
Un appareil photo est juste une boîte…
L'appareil photo n'est qu'un outil comme un ciseau.
Au photographe de sculpter une belle oeuvre avec.
Michio Oshino
Mes photos de coeur
L'appareil photo n'est qu'un outil comme un ciseau.
Au photographe de sculpter une belle oeuvre avec.
Michio Oshino
Mes photos de coeur
Merci pour toutes vos réponses et j'ai encore une question.
Mais auparavant je viens de retrouver dans le n° 292 (avril 2007) de Chasseur d'Images, une autre façon de calculer l'hyperfocale, soit in extenso:
" Le calcul de l'hyperfocale se fait en 2 étapes:
1- On commence par calculer le nombre K caractéristique de la Focale utilisée: K= F*F/30
2- On calcule ensuite la distance hyperfocale H par la formule suivante: H=K/f (f est l'ouverture du diaphragme)."
Cette formule vraisemblablement approximative a le mérite d'être facile à emmener aux champs dans sa tête. Qu'en pensez-vous ?
Maintenant ma question:
Pour une focale de 24mm, un diaphragme f/8, la formule ci-dessus donne 24*24/30/8= 2.40 m.
Appliquée à la lettre, une mise au point à 2.40 donnera une photo nette entre 1.20 m et l'infini.
Que se passe-t-il si au lieu de 2.40 m on règle la mise au point sur une valeur intermédiaire disons 4 mètres. La photo sera-t-elle nette de 2 m à l'infini ? avec la même finesse de détails ? Comment alors concilier cela avec la règle des 1/3 devant, 2/3 derrière ?
Mais auparavant je viens de retrouver dans le n° 292 (avril 2007) de Chasseur d'Images, une autre façon de calculer l'hyperfocale, soit in extenso:
" Le calcul de l'hyperfocale se fait en 2 étapes:
1- On commence par calculer le nombre K caractéristique de la Focale utilisée: K= F*F/30
2- On calcule ensuite la distance hyperfocale H par la formule suivante: H=K/f (f est l'ouverture du diaphragme)."
Cette formule vraisemblablement approximative a le mérite d'être facile à emmener aux champs dans sa tête. Qu'en pensez-vous ?
Maintenant ma question:
Pour une focale de 24mm, un diaphragme f/8, la formule ci-dessus donne 24*24/30/8= 2.40 m.
Appliquée à la lettre, une mise au point à 2.40 donnera une photo nette entre 1.20 m et l'infini.
Que se passe-t-il si au lieu de 2.40 m on règle la mise au point sur une valeur intermédiaire disons 4 mètres. La photo sera-t-elle nette de 2 m à l'infini ? avec la même finesse de détails ? Comment alors concilier cela avec la règle des 1/3 devant, 2/3 derrière ?
Un appareil photo est juste une boîte…
L'appareil photo n'est qu'un outil comme un ciseau.
Au photographe de sculpter une belle oeuvre avec.
Michio Oshino
Mes photos de coeur
L'appareil photo n'est qu'un outil comme un ciseau.
Au photographe de sculpter une belle oeuvre avec.
Michio Oshino
Mes photos de coeur
nico a écrit : Cela supposerait qu'a nombre de pixels identiques 1 capteur 24x36 a une meilleure profondeur de champs qu'1 APS, or dans la réalité c'est l'inverse.
qu'appelles-tu une bonne profondeur de champ : une profondeur grande ou faible ?
Si on pense généralement qu'un petit capteur a une plus grande PDC qu'un FF, c'est plutôt parce que, à même focale réelle, pour composer pareil, on se tient plus loin, et que la PDC augmente avec la distance.
Si on prend une distance et une ouverture données, l'APS a une PDC plus courte que le FF.
Revenir vers « Discussions générales sur les boîtiers »
Qui est en ligne ?
Utilisateurs parcourant ce forum : Aucun utilisateur inscrit et 3 invités